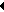| Історія математики | робоча програма | силабус |
| Історія математичної освіти | робоча програма | силабус |
| Математичний аналіз | робоча програма | силабус |
| Алгебра і теорія чисел | робоча програма | силабус |
| Лінійна алгебра | робоча програма | силабус |
| Аналітична геометрія | робоча програма | силабус |
| Диференціальна геометрія | робоча програма | силабус |
| Дискретна математика | робоча програма | силабус |
| Теорія ймовірностей та математична статистика | робоча програма | силабус |
| Елементарна математика | робоча програма | силабус |
| Методика навчання математики | робоча програма | силабус |
| Лінійна алгебра та аналітична геометрія (ФІ, ФМ) | робоча програма | силабус |
| Основи вищої математики (ЕКО-23) | робоча програма | силабус |
| Основи вищої математики (ХІ-23) | робоча програма | силабус |
| Лінійна алгебра та аналітична геометрія | робоча програма | силабус |
| Додаткові розділи математичного аналізу | робоча програма | силабус |
| Теорія ймовірностей та математична статистика | робоча програма | силабус |
| Дискретна математика | робоча програма | силабус |
| Основи теорії ймовірностей | робоча програма | силабус |
| Математична статистика в соціології | робоча програма | силабус |
| Теорія ймовірностей і математичні методи у психології | робоча програма | силабус |
| Математика та математична статистика | робоча програма | силабус |
- Автор: Кафедра математики та методики її навчання
- Перегляди: 1725